Contest
1. Form Smallest Number From Two Digit Arrays
Given two arrays of unique digits nums1 and nums2, return the smallest number that contains at least one digit from each array.
Example 1:
1
2
3
Input: nums1 = [4,1,3], nums2 = [5,7]
Output: 15
Explanation: The number 15 contains the digit 1 from nums1 and the digit 5 from nums2. It can be proven that 15 is the smallest number we can have.
Example 2:
1
2
3
Input: nums1 = [3,5,2,6], nums2 = [3,1,7]
Output: 3
Explanation: The number 3 contains the digit 3 which exists in both arrays.
Constraints:
1 <= nums1.length, nums2.length <= 91 <= nums1[i], nums2[i] <= 9- All digits in each array are unique.
My solution during the contest (AC)
1
2
3
4
5
6
class Solution:
def minNumber(self, nums1: List[int], nums2: List[int]) -> int:
n1, n2 = min(nums1), min(nums2)
if len(nums1) + len(nums2) == len(set(nums1 + nums2)):
return min(n1 * 10 + n2, n2 * 10 + n1)
return min(set(nums1).intersection(set(nums2)))
Better Solution 1: hash
1
2
3
4
5
6
7
class Solution:
def minNumber(self, nums1: List[int], nums2: List[int]) -> int:
s1, s2 = set(nums1), set(nums2)
s = s1 & s2
if s: return min(s)
x, y = min(nums1), min(nums2)
return min(x * 10 + y, y * 10 + x)
Better Solution 2: bit manipulation
1
2
3
4
5
6
7
8
9
10
11
12
func minNumber(nums1, nums2 []int) int {
var mask1, mask2 uint
for _, x := range nums1 { mask1 |= 1 << x }
for _, x := range nums2 { mask2 |= 1 << x }
if m := mask1 & mask2; m > 0 {
return bits.TrailingZeros(m)
}
x, y := bits.TrailingZeros(mask1), bits.TrailingZeros(mask2)
return min(x*10+y, y*10+x)
}
func min(a, b int) int { if b < a { return b }; return a }
2. Find the Substring With Maximum Cost
You are given a string s, a string chars of distinct characters and an integer array vals of the same length as chars.
The cost of the substring is the sum of the values of each character in the substring. The cost of an empty string is considered 0.
The value of the character is defined in the following way:
If the character is not in the string
chars, then its value is its corresponding position (1-indexed) in the alphabet.- For example, the value of
'a'is1, the value of'b'is2, and so on. The value of'z'is26.
- For example, the value of
Otherwise, assuming
iis the index where the character occurs in the stringchars, then its value isvals[i].
Return the maximum cost among all substrings of the string s.
Example 1:
1
2
3
4
5
Input: s = "adaa", chars = "d", vals = [-1000]
Output: 2
Explanation: The value of the characters "a" and "d" is 1 and -1000 respectively.
The substring with the maximum cost is "aa" and its cost is 1 + 1 = 2.
It can be proven that 2 is the maximum cost.
Example 2:
1
2
3
4
5
Input: s = "abc", chars = "abc", vals = [-1,-1,-1]
Output: 0
Explanation: The value of the characters "a", "b" and "c" is -1, -1, and -1 respectively.
The substring with the maximum cost is the empty substring "" and its cost is 0.
It can be proven that 0 is the maximum cost.
Constraints:
1 <= s.length <= 10^5sconsist of lowercase English letters.1 <= chars.length <= 26charsconsist of distinct lowercase English letters.vals.length == chars.length-1000 <= vals[i] <= 1000
My solution during the contest (AC)
Similar to 53. Maximum Subarray.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
def maximumCostSubstring(self, s: str, chars: str, vals: List[int]) -> int:
# construct all costs from 'a' to 'z'
cost = dict(zip(chars, vals))
for ascii in range(97, 123): # ord('a') = 97
alpha = chr(ascii)
if alpha not in cost:
cost[alpha] = ascii - 96
max_val = max(cost.values())
if max_val <= 0: # Empty substring
return 0
ans = res = 0
for char in s:
if cost[char] + res <= 0:
res = 0
continue
res += cost[char]
ans = max(ans, res)
ans = max(ans, res)
return ans
Better solution: dynamic planning
1
2
3
4
5
6
7
8
class Solution:
def maximumCostSubstring(self, s: str, chars: str, vals: List[int]) -> int:
mapping = dict(zip(chars, vals))
ans = f = 0
for c in s:
f = max(f, 0) + mapping.get(c, ord(c) - ord('a') + 1)
ans = max(ans, f)
return ans
3. Make K-Subarray Sums Equal
You are given a 0-indexed integer array arr and an integer k. The array arr is circular. In other words, the first element of the array is the next element of the last element, and the last element of the array is the previous element of the first element.
You can do the following operation any number of times:
- Pick any element from
arrand increase or decrease it by1.
Return the minimum number of operations such that the sum of each subarray of length k is equal.
A subarray is a contiguous part of the array.
Example 1:
1
2
3
4
5
6
7
8
Input: arr = [1,4,1,3], k = 2
Output: 1
Explanation: we can do one operation on index 1 to make its value equal to 3.
The array after the operation is [1,3,1,3]
- Subarray starts at index 0 is [1, 3], and its sum is 4
- Subarray starts at index 1 is [3, 1], and its sum is 4
- Subarray starts at index 2 is [1, 3], and its sum is 4
- Subarray starts at index 3 is [3, 1], and its sum is 4
Example 2:
1
2
3
4
5
6
7
8
Input: arr = [2,5,5,7], k = 3
Output: 5
Explanation: we can do three operations on index 0 to make its value equal to 5 and two operations on index 3 to make its value equal to 5.
The array after the operations is [5,5,5,5]
- Subarray starts at index 0 is [5, 5, 5], and its sum is 15
- Subarray starts at index 1 is [5, 5, 5], and its sum is 15
- Subarray starts at index 2 is [5, 5, 5], and its sum is 15
- Subarray starts at index 3 is [5, 5, 5], and its sum is 15
Constraints:
1 <= k <= arr.length <= 10^51 <= arr[i] <= 10^9
My solution during the contest (WRONG)
My idea is wrong, because we can add or sub any of these numbers alternately.
See the correct solution after this.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# NOTE: It's WRONG!!!!!
class Solution:
def makeSubKSumEqual(self, arr: List[int], k: int) -> int:
n = len(arr)
if n <= 1:
return 0
arr_min = min(arr)
for i in range(n):
arr[i] -= arr_min
arr += [arr[i] for i in range(k - 1)]
pre_sum = [0]
pre_sum.extend(pre_sum[-1] + num for num in arr)
# Make K-Subarray Sums Equal
sums = [0] * n
for i in range(n):
sums[i] = pre_sum[i + k] - pre_sum[i]
sums0 = copy.deepcopy(sums)
add_ops = sub_ops = 0
# Always add
while min(sums) != max(sums):
sums_min = min(sums)
sums_max = max(sums)
idx = sums.index(sums_min)
for i in range(idx, idx + k):
sums[i % n] += sums_max - sums_min
add_ops += sums_max - sums_min
# Always sub
while min(sums0) != max(sums0):
sums_min = min(sums0)
sums_max = max(sums0)
idx = sums0.index(sums_max)
for i in range(idx, idx + k):
sums0[i % n] -= sums_max - sums_min
sub_ops += sums_max - sums_min
return min(add_ops, sub_ops)
Better solution
For convenience, let’s simplify “arr” as “a”.
Hint 1
First, let’s solve the case where a is not a circular array.
According to the problem statement, consider two subarrays of length k starting at indices i and i+1. If the sum of these two subarrays is required to be equal, then we have the following equation:
a[i] + a[i+1] + ... + a[i+k-1] = a[i+1] + a[i+2] + ... + a[i+k]
Simplifying this equation gives:
a[i] = a[i+k]
In other words,
a[0] = a[k] = a[2k] = ...a[1] = a[k+1] = a[2k+1] = ...a[2] = a[k+2] = a[2k+2] = ...
And so on.
Hint 2
Group the elements of a according to the result of mod i mod k. For each group (denoted by b), we need to solve the minimum number of operations required to make all elements of b equal.
According to the median greedy algorithm, it is optimal to set all elements of b to the median of b.
Proof:
Let the length of b be m. If x is chosen from the interval [b[0], b[m-1]], then the distance between x and the leftmost and rightmost elements of b is always equal to b[0] + m - 1 - b[m-1] = m - 1. Therefore, x can only be chosen from the middle m/2 elements of b.
If x is chosen from the other interval [b[m-1], b[0]], then the distance between x and the leftmost and rightmost elements of b is always equal to b[m-1] + m - 1 - b[0] = m - 1. Therefore, x can only be chosen from the middle m/2 elements of b, regardless of whether x is in the first or second interval.
Therefore, x can only be chosen from the middle m/2 elements of b.
Hint 3
Back to the original array a in the original problem statement since a is a circular array.
1
2
3
4
5
6
7
8
9
class Solution:
def makeSubKSumEqual(self, arr: List[int], k: int) -> int:
k = gcd(k, len(arr))
ans = 0
for i in range(k):
b = sorted(arr[i::k])
mid = b[len(b) // 2]
ans += sum(abs(x - mid) for x in b)
return ans
4. Shortest Cycle in a Graph
There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1. The edges in the graph are represented by a given 2D integer array edges, where edges[i] = [ui, vi] denotes an edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
Return the length of the shortest cycle in the graph. If no cycle exists, return -1.
A cycle is a path that starts and ends at the same node, and each edge in the path is used only once.
Example 1:

1
2
3
Input: n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]]
Output: 3
Explanation: The cycle with the smallest length is : 0 -> 1 -> 2 -> 0
Example 2:
1
2
3
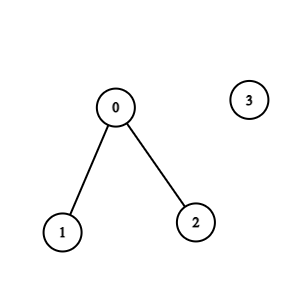
Input: n = 4, edges = [[0,1],[0,2]]
Output: -1
Explanation: There are no cycles in this graph.
Constraints:
2 <= n <= 10001 <= edges.length <= 1000edges[i].length == 20 <= ui, vi < nui != viThere are no repeated edges.
My solution during the contest
1
None
Better solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
def findShortestCycle(self, n: int, edges: List[List[int]]) -> int:
g = [[] for _ in range(n)]
for x, y in edges:
g[x].append(y)
g[y].append(x) # 建图
def bfs(start: int) -> int:
dis = [-1] * n # dis[i] 表示从 start 到 i 的最短路长度
dis[start] = 0
q = deque([(start, -1)])
while q:
x, fa = q.popleft()
for y in g[x]:
if dis[y] < 0: # 第一次遇到
dis[y] = dis[x] + 1
q.append((y, x))
elif y != fa: # 第二次遇到
# 由于是 BFS,后面不会遇到更短的环,直接返回
return dis[x] + dis[y] + 1
return inf # 该连通分量无环
ans = min(bfs(i) for i in range(n))
return ans if ans < inf else -1